#ResearchHighlight
🛎 Signatures of a sampling quantum advantage in driven quantum many-body systems
📌 Authors: Jirawat Tangpanitanon 1,2,3,12,*, Supanut Thanasilp 1,4,5,12,*, Marc-Antoine Lemonde 1,6, Ninnat Dangniam 5,7,8,9, and Dimitris G Angelakis 1,10,11,*
1: Centre for Quantum Technologies, National University of Singapore, Singapore
2: Quantum Technology Foundation (Thailand), Bangkok, Thailand
3: Thailand Center of Excellence in Physics, Ministry of Higher Education, Science, Research and Innovation, Bangkok, Thailand
4: Institute of Physics, Ecole Polytechnique Fédérale de Lausanne (EPFL), Switzerland
5: Chula Intelligent and Complex Systems, Department of Physics, Faculty of Science, Chulalongkorn University,
Thailand
6: Nord Quantique, P1-ACET 3000 Blvd Université, Sherbrooke, Canada
7: Department of Physics and Center for Field Theory and Particle Physics, Fudan University, China
8: State Key Laboratory of Surface Physics, Fudan University, China
9: The Institute for Fundamental Study (IF), Naresuan University, Thailand
10: School of Electrical and Computer Engineering, Technical University of Crete, Greece
11: AngelQ Quantum Computing, Singapore
12: The first two authors contributed equally.
∗Authors to whom any correspondence should be addressed.
📌 ความสำคัญและที่มา
เครื่องจำลองควอนตัมเชิงอนาล็อกคือแพลตฟอร์มทางควอนตัมที่เราสามารถควบคุมและนำไปใช้ในการจำลองพลวัตรของระบบควอนตัมหลายวัตถุได้ แต่ในขณะที่เครื่องจำลองควอนตัมเชิงอนาล็อกได้ช่วยให้คำตอบกับคำถามที่สำคัญหลายคำถามในฟิสิกส์ของระบบควอนตัมหลายวัตถุที่เราไม่สามารถหาได้จากเทคนิคเชิงตัวเลข (numerics) ที่มีอยู่ ข้อพิสูจน์ที่รัดกุมของอุตมภาคเชิงควอนตัม (quantum advantage) สำหรับระบบอนาล็อกยังจำกัดอยู่กับระบบที่ถูกออกแบบมาอย่างเฉพาะเจาะจงเท่านั้น
ผู้วิจัยได้ให้หลักฐานทางทฤษฎีว่าคอมพิวเตอร์แบบคลาสสิกไม่สามารถจำลองการสุ่มตัวอย่างบิตสตริงจากพลวัตรแบบคาบของตัวกระทำการที่สุ่มมาจากเซอร์คิวลาออโธกอนอลอองซองค์เบิล (COE) ได้ ตามสมมติฐานการเข้าสู่สมดุลความร้อนของสถานะไอเกน (eigenstate thermalization hypothesis – ETH) แล้ว COE เป็นอองซองค์เบิลของเมทริกซ์สุ่มที่อธิบายสมบัติทางสถิติของคลาสใหญ่ของระบบควอนตัมเชิงอนาล็อกที่ถูกขับเคลื่อน (driven) ในสมดุลความร้อน ผู้วิจัยได้สนับสนุน ETH โดยการศึกษาระบบอีซิ่งและระบบโบส-ฮับบาร์ดในหนึ่งมิติที่ถูกขับเคลื่อนแบบคาบ ซึ่งผลเชิงตัวเลขที่ได้ชี้ว่าระบบเหล่านี้อาจเป็นทางเลือกในการแสดงอุตมภาคควอนตัมที่ทำได้จริงในทางปฏิบัติ
งานวิจัยนี้ให้คำชี้แจงเกี่ยวกับความซับซ้อนทางการคำนวณไม่เฉพาะกับระบบที่เจาะจงแต่กับทั้งคลาสของระบบควอนตัมในสถานะของสสารเดียวกัน (ในที่นี้คือสถานะของสสารในสมดุลความร้อน) ผลการวิจัยนี้เป็นที่น่าสนใจในวงการทดลองเนื่องจากระบบที่ถูกขับเคลื่อนแบบคาบได้ถูกสร้างขึ้นจริงด้วยฮาร์ดแวร์ควอนตัมที่มีอยู่ในปัจจุบันแล้ว โดยเมื่อเร็วๆ นี้ การสุ่มค่าบิตสตริงจากระบบโบส-ฮับบาร์ดที่ถูกขับเคลื่อนในสมดุลความร้อนได้ถูกทดลองบนแพลตฟอร์มอะตอมที่เย็นจัด (ultra-cold) ที่ควบคุมได้ถึง 32 ตำแหน่งและ 20 อะตอม
📌 ผลสัมฤทธิ์สำคัญ
– ผู้วิจัยให้หลักฐานเชิงวิเคราะห์ของความยากในการจำลองการสุ่มตัวอย่างจากพลวัตรแบบ COE
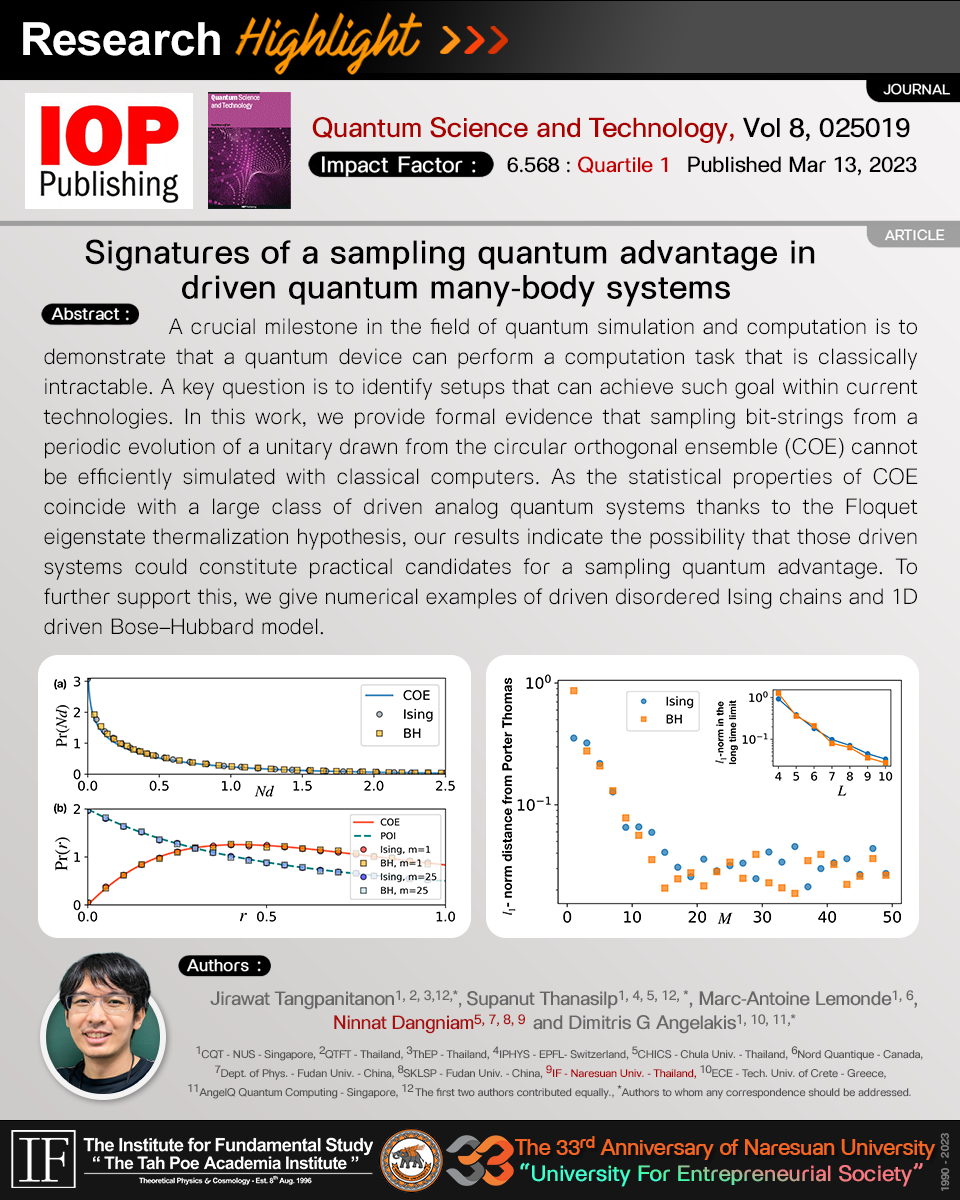
– ผู้วิจัยให้ผลลัพธ์เชิงตัวเลขซึ่งแสดงว่าระบบอีซิ่งและโบส-ฮับบาร์ดที่ถูกขับเคลื่อนในระยะของมีพารามีเตอร์ที่ทำได้จริงในการทดลองสามารถให้ผลเข้าใกล้สถิติแบบ COE และการแจกแจงแบบพอร์เตอร์-โธมัส (Porter-Thomas) ได้อย่างรวดเร็ว
📌 Motivation and background
Analog quantum simulators are controllable quantum platforms built to implement complex quantum many-body models, and they have been used to implement complex quantum dynamics that cannot be reproduced with existing classical numerics. While analog quantum simulators have shed light on important questions in quantum many-body physics, rigorous proof of a quantum advantage involving complexity theory in those analog systems is limited to specific models.
We have provided formal evidence that sampling bit-strings from a periodic evolution of a unitary drawn from the circular orthogonal ensemble (COE) cannot be efficiently simulated with classical computers assuming a standard computational complexity assumption. The COE is a random matrix ensemble that describes the statistical properties of a large class of driven analog quantum systems in the thermalized phase according to an eigenstate thermalization hypothesis (ETH). To bolster our support for the ETH, we numerically examined specific examples of driven disordered Ising chains and 1D driven Bose-Hubbard model. Our findings suggest that these driven systems could be practical candidates for a sampling quantum advantage.
This research provides a complexity statement not only on a particular model but on an entire class of analog quantum systems when they are in the same quantum phase. The findings are of broad interest to the experimental community as periodically driven systems have been implemented experimentally with current available quantum hardware. Recently, sampling from a driven thermalized Bose-Hubbard model has been experimentally implemented with an ultra-cold atom platform up to 32 sites and 20 atoms.
📌 Key results
– We give analytical evidence of the computational hardness of sampling from the COE dynamics.
– We provide numerical results showing that COE statistics and reaching the anti-concentrated Porter-Thomas distribution with polynomially many cycles can be obtained from driven quantum Ising and Bose-Hubbard models for realistic parameters.
📌 Journal :
https://iopscience.iop.org/article/10.1088/2058-9565/acbd69
#QIS #IFNU #PhysicsNaresuan
