Double dimensional reduction of M5-brane action in Sen formalism

#ResearchHighlight

🛎 Double dimensional reduction of M5-brane action in Sen formalism

📌 Authors: Anajak Phonchantuek*,** and Pichet Vanichchapongjaroen*

*The Institute for Fundamental Study “The Tah Poe Academia Institute”, Naresuan Univ., Thailand
**Development and Promotion of Science and Technology Talents Project (DPST Scholar)

📌 ความสำคัญและที่มา

การสร้างแอคชันสำหรับ เอ็ม5-เบรน ที่สมบูรณ์ ซึ่งคู่ควบกับพื้นหลังคือซูเปอร์กราวิตีสิบเอ็ดมิติ ไม่สามารถทำอย่างตรงไปตรงมาได้ สาเหตุสำคัญสาเหตุหนึ่งมาจากการมีอยู่ของสนาม 2-ฟอร์ม ที่มีความเข้มสนาม 3-ฟอร์ม ซึ่งคู่กันกับตัวเอง โดยสนามดังกล่าวเป็นหนึ่งในสนามบน เอ็ม5-เบรน แม้แต่การสร้างแอคชันสำหรับสนามดังกล่าวก็ไม่อาจทำอย่างตรงไปตรงมาได้ วิธีการมาตรฐานวิธีหนึ่งที่จะสร้างแอคชันดังกล่าว และนำไปขยายผลสร้างแอคชันเอ็ม5-เบรน ที่สมบูรณ์ได้ คือวิธีการของ PST วิธีการดังกล่าวนิยามสนามช่วยซึ่งไม่มีพลวัต เมื่อไม่นานมานี้ มีอีกวิธีหนึ่งซึ่งเรียกว่าวิธีการของ Sen วิธีการนี้มีพื้นฐานมาจากผลของทฤษฎีสนามสตริง ในวิธีนี้ สนาม 2-ฟอร์ม ที่มีความเข้มสนาม 3-ฟอร์ม ไม่ใช่สนามไม่ผสม แต่ประกอบขึ้นจากสนาม 2-ฟอร์ม P และสนาม 3-ฟอร์ม Q ซึ่งทั้งสองสนามแปลงแบบไม่ปกติภายใต้การแปลงพิกัด แอคชันที่ประกอบขึ้นมาจากสนาม P และ Q สามารถสร้างได้ และขยายผลไปสร้างแอคชันสำหรับ เอ็ม5-เบรน ที่สมบูรณ์ได้

แม้ว่าการสร้างแอคชันสำหรับ เอ็ม5-เบรน ที่สมบูรณ์โดยใช้วิธีการของ Sen สามารถทำได้ แต่แอคชันดังกล่าวอยู่ในรูปแบบที่ยากต่อการศึกษา เนื่องจากมีการคู่ควบกับความโน้มถ่วงในลักษณะที่ซับซ้อนเป็นอย่างมาก วิธีการหนึ่งที่จะช่วยทำให้เข้าใจแอคชันดังกล่าวมากขึ้น คือการศึกษาการลดมิติ ในงานวิจัยนี้ เราเน้นศึกษาการลดมิติทั้งสองส่วนของแอคชัน เอ็ม5-เบรน บนวงกลม กล่าวคือ หนึ่งในมิติของพื้นหลังมีลักษณะเป็นวงกลม และหนึ่งในมิติของ เอ็ม5-เบรน จะพันรอบวงกลมดังกล่าว นอกจากนี้ งานวิจัยนี้ยังสนใจการศึกษาการขยายผลของการลดมิติทั้งสองส่วนสำหรับปริภูมิในลักษณะอื่น ๆ ด้วย

📌 ผลสัมฤทธิ์สำคัญ

– เราแสดงให้เห็นว่าการลดมิติทั้งสองส่วนของแอคชัน Sen ที่เป็นกำลังสองใน 6 มิติ บนวงกลม จะให้ทฤษฎีแม็กซ์เวลล์ใน 5 มิติ ทั้งหมดสองทฤษฎี ซึ่งมีเครื่องหมายของพลังงานจลน์แตกต่างกัน สนามแม็กซ์เวลล์ที่มีเครื่องหมายของพลังงานจลน์ที่ถูกต้อง มีการสเกลในลักษณะ 1/r โดยที่ r เป็นรัศมีของวงกลม ผลดังกล่าวสอดคล้องกับสมมาตรคงแบบ

– เราแสดงให้เห็นว่าการลดมิติทั้งสองส่วนของแอคชัน เอ็ม5-เบรน แบบ Sen บนวงกลม จะให้ทฤษฎีที่สมบูรณ์ของ ดี4-เบรน หรือ คู่ของดี4-เบรน ขึ้นอยู่กับวิธีการเลือกตัวดำเนินการฉายที่เหมาะสม

– เราเสนอขั้นตอนวิธีในการขยายผลของการลดมิติทั้งสองส่วนบนปริภูมิในลักษณะอื่น จากนั้น เราแสดงให้เห็นว่าขั้นตอนวิธีดังกล่าวใช้ได้ผลกับการศึกษาแอคชันกำลังสองที่พันรอบทอรัส ในตัวอย่างนี้ เราตีความได้ว่า ภาวะคู่กันแบบ S สำหรับทฤษฎีลดมิตินั้น เป็นผลมาจากการสลับตัวดำเนินการฉายในทฤษฎีเต็ม

📌 Motivation and background

The construction of a complete M5-brane action coupled to the background eleven-dimensional supergravity is non-trivial. This is largely due to a 2-form field with 3-form self-dual field strength, which is one of the degrees of freedom on M5-brane. The construction of a worldvolume action of this field itself is readily not straightforward. A standard way to remedy this which allows the extension to a complete M5-brane action is called the PST formalism. In this formalism, auxiliary fields with no dynamics are introduced. More recently, there is an alternative approach which is called the Sen formalism. This formalism is motivated from a result in string field theory. The independent field in this formalism are a 2-form field P and a 3-form field Q, both of which transform in non-standard way under diffeomorphism. In this formalism, the 2-form field with self-dual field strength is a composite field consisting of P and Q. It is possible to extend this construction to a complete M5-brane action in Sen formalism.

Although the construction of an M5-brane action in Sen formalism has been successful, the action itself is not easy to work with due to the complicated way in which it couples to gravity. One way to better understand the action and to understand how it couples to gravity is to study dimensional reduction. In this paper, we focus on double dimensional reduction of an M5-brane action on a circle. This means that one of the spatial dimensions of the background target space is compactified on a circle. Then, one of the spatial dimensions of the M5-brane worldvolume is wrapped around this circle. The generalisation for double dimensional reduction on some other spaces are also studied.

📌 Key results

– We have shown that double dimensional reduction of 6d Sen quadratic action on a circle gives a theory of two uncoupled Maxwell fields of opposite sign of kinetic terms. The field with correct sign of kinetic term scales like 1/r, where r is the radius of the circle. This result is as expected by the conformal symmetry.

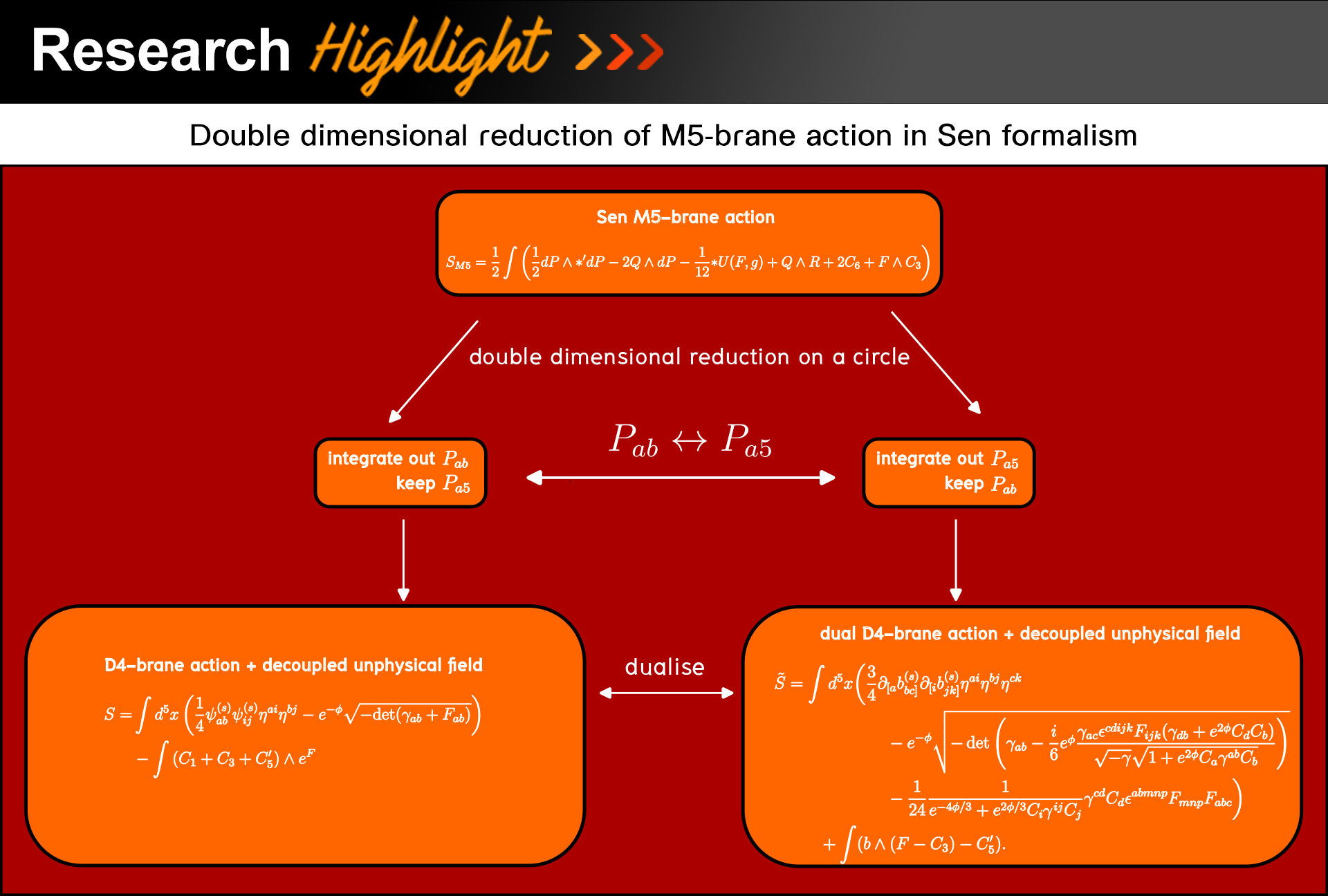
– We have explicitly shown that double dimensional reduction of the Sen M5-brane action on a circle gives rise to the complete D4-brane action or the complete dual D4-brane action, depending on how projection operators are chosen.

– We have proposed an algorithm to compute double dimensional reduction of the Sen M5-brane action on some other spaces. We have shown that this algorithm is applicable to the quadratic action compactified on a torus. In this example, the S-duality of the reduced theory is simply a realisation of the swapping of projection operators in the full theory.

📌 Journal : https://link.springer.com/article/10.1140/epjc/s10052-023-11892-2

#IFTHEP #IFNU #PhysicsNaresuan