Research interests
A bird's eye view on what I am searching for....
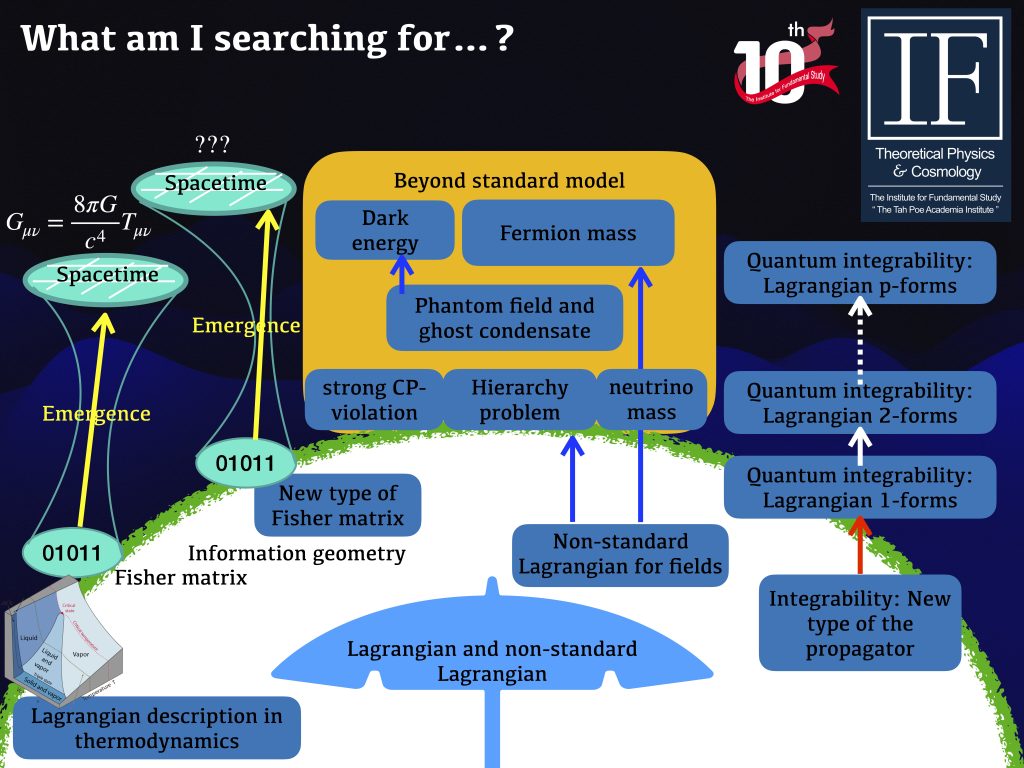
Research topics
1) Integrability and multi-dimensional consistency
An integrable system is a mathematical model that can be solved exactly using certain mathematical methods. In more specific view, an untenable system is a system of differential (different) equations that can be solved by means of the inverse scattering transform, the Bethe ansatz, or other methods that allow for explicit expressions of solutions in terms of integrals. One of the key properties of integrable systems is the presence of an infinite number of conserved quantities, known as the Liouville's integrability, which are related to symmetries of the system. These conserved quantities allow for the preservation of certain properties of the system over time, and can provide insight into its long-term behaviour. A key integrable feature in this context is the Hamiltonian commuting flows. Moreover, untenable systems are also characterised by the absence of chaos (irregular pattern), which means that small perturbations do not lead to unpredictable behaviour.
Multi-dimensional consistency refers to the property of integrable systems in which the equations of motion for different components of the system are compatible with each other in multi-dimension. In other words, the equations for each component are consistent with each other, so that a solution for one component uniquely determines a solution for the others. This property ensures that the behaviour of the system can be predicted exactly and with complete accuracy, making integrable systems particularly useful for mathematical and theoretical analysis. Nowadays, the multi-dimensional consistency is a hallmark of integrable systems and is a key feature that distinguishes them from non-integrable systems.
Another important notion of integrability is the Lagrangian multi-form which was recently developed in the past 10 years. Lobb and Nijhoff first set out to formulate the discrete theory for 2-form and 3-form cases. A key relation in this context is the Lagrangian closure relation (equivalently with Hamiltonian commuting flows), which holds on the solution of the system, as a direct result of the variation of the action with respect to independent variables. The existence of the Lagrangian closure relation guarantees the constant value of the action under local deformation of the surface in the 2-form case and the volume in the 3-form case on the space of independent variables. Soon later, the 1-form case was formulated by Yoo-Kong, Lobb and Nijhoff (Here is my PhD thesis) in both discrete and continuous levels through an important integrable model known as the Calogero-Moser system. Again, the existence of the Lagrangian 1-form closure relation guarantees the constant value of the action under local deformation of the curve on the space of independent variables. Therefore, the feature implies path-independent property and the multi-time evolution does not depends on the choice of paths, but rather the end points on the space of independent variables. Indeed, this is nothing but the multi-dimensional consistency feature which is represented in the level of Lagarngians (Of course, Hamiltonian commuting flows can be also treated as the multi-dimensional consistency on the level of Hamiltonians). After these pioneer works, a series of papers has been producing and pushing further in various aspects as well as various systems.
In quantum arena, the notion of integrability is not well established. Naively, one can follow the canonical quantisation by promoting a set of invariances or a set of Hamiltonians to be a set of Hamiltonian operators. Therefore, the integrability demands commutator of the Hamiltonian operators to be zero. However, Weight provided an encounter example, which is non-integrable system, satisfying the vanishing commutator condition. However, many attempts have been put further to investigate quantum integrability on demanding a quantum correction terms promoted from the invariances of the counterpart of classical system and commutations of them. In discrete level, a key tool to study quantum integrable system us the quantum mapping was established and was applied in the integrability context. Alternatively, Feynman approach on quantising the system might be a better choice. The pioneer works on this direction were investigated by Field and Nijhoff in the discrete systems. In 2019, King and Nijhoff set out to formulate quantum path integration incorporated with the quadratic Lagrangian multi-form structure in the discrete level.
Recently, we successfully construct the continuous muti-time propagator for the case of Lagrangian 1-forms, see "
Quantum integrability: Lagrangian 1-form" (2023). With this new type of the propagator, a new paradigm on summing over possible paths is introduced since one needs to take into account both all possible paths on the space of dependent variables and the space of independent variables. The integrability notion in terms of the multi-dimensional consistency is captured through the path independent feature of the evolution on the space of independent variables known as the quantum variational principle.
-
Of course, with this very first brick on constructing the propagator associated with Lagrangian 1-forms, one can pursue the higher-form case to establish the integrability condition.
#MSc/PhD research topics are available.
#Self-Funded or externally sponsored students are welcome to join the project.
#Partially-Funded scholarships are available for PhD students.
------------------------------------------------------------------------------------------------------------------------------------------
2) Non-standard Lagrangian and its application in field theory
-
In classical mechanics, Lagrangian is typically defined as the difference between the kinetic energy and potential energy of the system and we shall call this type of Lagrangians as a standard. form. Inserting the Lagrangian into the Euler-Lagrange equation, one obtains the equation(s) of motion (EOM). Of course, a non-standard Lagrangian is the one that does not possess the usual form of the kinetic energy minus the potential energy. Such Lagrangians may contain additional terms, e.g. higher-oder derivative terms, or may be defined in a completely different way. Non-standard Lagrangians also arise in the context of field theory to describe the interactions of particles and fields. Traditionally, higher-order derivative terms and complex interaction terms were added by hand without symmetry violation.
-
In 2016,
Sarawuttinack and Yoo-Kong proposed a new form of Lagrangian, called the multiplicative Lagrangian, in the case of one degree of freedom. Naively, this Lagrangian is in the product form between a function of velocity and a function of potential. A point is that Lagrangian has been treated as a solution of the Euler-Lagrange equation. Solving this new type of Lagrangian by employing the separation variable method, one obtains an explicit form. A key feature is that this multiplicative Lagrangian comes with a parameter and under an appropriate limit on this parameter, the standard Lagrangian is recovered. Moreover, if we consider the series expand of the multiplicative Lagrangian with respect to the parameter, the Lagrangian hierarchy is constructed. Of course, all Lagrangians in the hierarchy give the identical EOM of the system. Then with this structure of the multiplicative Lagrangian, it would provide a new light to the non-uniqueness property of the Lagrangian. In other words, we find a systematical way to write various forms of the Lagrangian producing the same EOM.
-
The standard model of particle physics (SMPP) is a well-established theory that describes the fundamental particles and their interrelations. However, there are some phenomena that cannot be explained by the SMPP, such as dark matter, dark energy, the hierarchy problem, strong CP problem, neutrino mass, quantising gravity and the baryon asymmetry problem. In the past years, physicists have proposed several theories that go beyond the SMPP, including:
- Supersymmetry (SUSY): This theory proposes that each known particle in the SMPP has a supersymmetric partner, which has a different spin. SUSY could solve the hierarchy problem and provide a candidate for dark matter.
- Grand Unified Theories (GUTs): These theories attempt to unify the strong, weak and electromagnetic interactions to a single framework. GUTs predict new particles and interactions, which could be observed at high energies.
- Extra Dimensions: These theories propose that there may be more than the three spatial dimensions and one temporal dimension that we experience. Extra dimensions could explain why gravity is so weak comparing to other interactions and could also solve the hierarchy problem.
- String Theory: This theory proposes that the fundamental building blocks of the universe is not particles, but tiny vibrating strings. String theory provides a way to construct a graviton. However, there is a price to pay which is an extra-dimension.
Recently, Supanyo and Yoo-Kong proposed a new form of the Lagrangian, namely the multiplicative form of the complex scalar field, to provide alternative explanation to the hierarchy problem and strong CP problem. For the hierarchy problem associated with the Higgs mass, the new form of the Lagrangian can provide a tiny quantum correction and a bare mass of the Higgs particle is in the same order with the observation 125 GeV. This means that , with this new way to write the Lagrangian, one needs no fine tuning. For the strong CP problem, our model can naturally explain the phenomenon without introducing a new hypothetical particle such as an axion.
With this new way of looking problems, there is a high potential for the multiplicative Lagrangian to give an alternative explanation to other problems in the realm of the beyond standard model of particles physics.
#MSc/PhD research topics are available.
#Self-Funded or externally sponsored students are welcome to join the project.
#Partially-Funded scholarships are available for PhD students.
------------------------------------------------------------------------------------------------------------------------------------------
3) Information geometry
-
Information geometry is a branch of mathematics that studies the geometric structure and properties of information spaces (probability manifolds). It is based on the idea that information can be represented mathematically as probability distributions, and that the properties of these distributions can be analyse using tools from differential geometry. In this context, probability distributions are treated as points in a geometric space, where the geometry of the space, e.g. curvature, is determined by the properties of the distributions. The distance between two points on the probability manifold is measured using a metric known as a Fisher-Rao matrix. Intriguingly, the matrix can be obtained from the Kullback-Leibler divergence, a.k.a the relative entropy, by considering the first order of the expansion if two points are infinitesimally close. Information geometry has a wide range of applications, ranging from statistical inference, machine learning to neural networks.
-
Recently,
Bukaew and Yoo-Kong proposed a one-parameter Fisher-Rao matrix for one-random variable case. To obtain such a new Fisher-Rao matrix, one employ a connection between the action functional and Fisher information together with the multiplicative form of Lagrangian. Of course, under an appropriate limit on the parameter, a standard Fisher-Rao matrix is recover. Moreover, if we consider the a series expansion with respect to the parameter, one obtains the metric hierarchy and, of course, the standard Fisher-Rao metric is the first one in the hierarchy. A interesting feature is that this new Fisher-Rao matrix comes with the parameter which could be treated as a Tasllis's index connecting with non-additivity property.
-
Of course, one can try to extend the idea to the case of many random variables. The application of this new type of Fisher-Rao matrix is still open. However, one active research area to understand a nature of spacetime is the emergent phenomenon of space and time from information might be found a usefulness from this one-parameter Fisher-Rao matrix. Specifically, one can derive the Einstein field equation from Fisher information. Then one could ask what would we obtain with the one-parameter Fisher information?
-
#MSc/PhD research topics are available.
#Self-Funded or externally sponsored students are welcome to join the project.
#Partially-Funded scholarships are available for PhD students.
------------------------------------------------------------------------------------------------------------------------------------------
4) Second law of thermodynamics and entanglement
-
Quantum thermodynamics is a branch of physics that combines that principles of quantum mechanics and thermodynamics to describe the behaviour of small, quantum mechanical systems. It aims to extend the laws of thermodynamics to the microscopic world of individual atoms and particles, where quantum effects are playing a key role e.g. entanglement. Classically, the second law of thermodynamics states that in any natural thermodynamics process, the total entropy, defined through heat and temperature of the system, of a closed system will always tend to increase over time. Entropy can be thought of as a measure of the randomness of a system, and the second law implies that over time, natural processes will tend to move towards states of greater entropy. In quantum thermodynamics, the concepts of works, heat, and energy are redefined in terms of the underlying quantum mechanics of the system, e.g. work is defined as the change in energy of a quantum mechanical system caused by the manipulation of its Hamiltonian, while heat is defined as the energy exchange between a quantum systems and its environment due to temperature differences.
-
Recent developments in this context show that the second law of thermodynamics seems to be possibly violated. In simple words, in quantum realm, heat can naturally flow from a cold body to a hot body. However, in fact, the second law of thermodynamics is still intact since one needs to take into account the consumption of entanglement between the hot and cold bodies. The entropy of spending entanglement of the system will compensate the missing entropy and, therefore, entropy of the whole system will increase while the heat flows backwards.
-
#MSc/PhD research topics are available.
#Self-Funded or externally sponsored students are welcome to join the project.
#Partially-Funded scholarships are available for PhD students.
------------------------------------------------------------------------------------------------------------------------------------------
5) Lagrangian description in thermodynamics and classical statistical mechanics
-
Traditionally, in thermodynamics, the way to describe the system is through the equation of state (EOS). There is not equation of motion (EOM) of the system like those in the classical mechanics as a result of least action principle. However, with notion of differential forms, one can analogy the EOS in thermodynamics with EOM in classical mechanics. This might give us a way to construct a new way to study thermodynamics in the same language with the classical mechanics while keeping path-independent feature of the thermodynamic process intact.
-
-
Very recently, I figure out how to formulate the classical statistical ensemble with the Lagrangian formalism. A key magic trick is a Wick's rotation, like those in the case of the path integration but there is a different, allowing us to formulate the Lagrangian version of the Liouville's theorem. Therefore, a definition of the microcanonical and canonical ensembles can be defined. With a simple system, one dimension harmonic oscillator, we can show that on computing physical quantities, e.g. entropy and partition function, both Hamiltonian and imaginary-time Lagrangian give identical results, see "
Lagrangian formalism and classical statistical ensemble".
-
#MSc/PhD research topics are available.
#Self-Funded or externally sponsored students are welcome to join the project.
#Partially-Funded scholarships are available for PhD students.
------------------------------------------------------------------------------------------------------------------------------------------
6) Quantisation of the thermodynamic systems
- Thermodynamics is the branch of physics that deals with heat, work, and the forms of energy transfer within physical systems at the macroscopic level. It focuses on how energy moves between different states and how it impacts matter, particularly in terms of changes in temperature, pressure, and volume.Thermodynamics is governed by a set of fundamental principles known as the Four Laws of Thermodynamics, which describe how these quantities behave in various situations.
A question: Can thermodynamics go quantum ?
Well....Yes. And this field is rapidly flourishing.
Quantum thermodynamics is a field of study that combines principles from quantum mechanics and thermodynamics to understand how energy, work, and heat behave in systems governed by quantum laws. It extends classical thermodynamics to the quantum scale, where the behavior of particles and energy levels are fundamentally different due to quantum effects like superposition, entanglement, and discreteness of energy states.
However, what I have in mind is not exactly the same thing above. My question is "Can we quantise a thermodynamic system?" This question is might sound weird since thermodynamics is dealing with large classical systems, one might wonder what do you mean by saying about its quantum version. An interesting fact is that there is analogue structure between Hamiltonian mechanics and Thermodynamics, see John Baez. This intriguing connection would allow us to construct the thermodynamic phase space and of course, possibly, one might try to construct a quantum theory from this structure, like we did in the case of the classical mechanics.
------------------------------------------------------------------------------------------------------------------------------------------
7) Any topic that I can do math!
------------------------------------------------------------------------------------------------------------------------------------------
Selected publications
- Sikarin Yoo-Kong, Sarah Lobb and Frank Nijhoff, 2011, “Discrete-time Calogero-Moser system and Lagrangian 1-form structure ”, Journal of Physics A: Mathematical and Theoretical, 44, 365203
- Kittikun Surawuttinack, Sikarin Yoo-Kong and Monsit Tanasittikosol, 2016, “Multiplicative form of the Lagrangian”, Theoretical and Mathematical Physics, 189(3), pp.1693-1711
- Suppanat Supanyo, Monsit Tanasittikosol, and Sikarin Yoo-Kong, 2022, "Natural TeV cutoff of the Higgs field from a multiplicative Lagrangian", Physical Review D, 106(3), 035020.
- Tanadon Kongkoom and Sikarin Yoo-Kong, 2023, "Quantum integrability: Lagrangian 1-form case", Nuclear Physics B, 987, 116101.
- Worachet Bukaew and Sikarin Yoo-Kong, 2023, "One-parameter generalised Fisher information matrix: One random variable", Reports on Mathematical Physics, 91(1), pp. 57-78.
- Publication list [Google Scholar Citations]
Articles
Research grants
- King Mongkut’s University of Technology Thonburi Research Grant 2012
- Thailand Toray Science Foundation (TTSF) 2013
- Faculty of Science, King Mongkut’s University of Technology Thonburi Research Grant 2013
- The Thailand Research Fund (TRF): New Researcher 2013
- National Research Council of Thailand (NRCT) 2013
- National Research Council of Thailand (NRCT) 2014
- National Research Council of Thailand (NRCT) 2015
- National Research Council of Thailand (NRCT) 2017
- JSTP 2019-2020
